Giải bài tập Bài 10 trang 128 Toán 11 Tập 1 | Toán 11 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 10 trang 128 Toán 11 Tập 1. Bài tập cuối chương 4. Toán 11 - Chân trời sáng tạo
Đề bài:
Bài 10 trang 128 Toán 11 Tập 1: Cho hình chóp SABCD với ABCD là hình thoi cạnh a, tam giác SAD đều. M là điểm trên cạnh AB, (α) là mặt phẳng qua M và (α) // (SAD) cắt CD, SC, SD lần lượt tại N, P, Q.
a) Chứng minh rằng MNPQ là hình thang cân.
b) Đặt AM = x, tính diện tích MNPQ theo a và x.
Đáp án và cách giải chi tiết:
Do (α) đi qua M và (α) // (SAD) nên (α) cắt các mặt của hình chóp tại các giao tuyến song song với (SAD).
+) Trong mặt phẳng (ABCD), từ điểm M kẻ đường thẳng song song với AD cắt CD tại N. Suy ra giao tuyến của (α) và (ABCD) là MN // AD.
+) Trong mặt phẳng (SCD), từ điểm N kẻ đường thẳng song song với SD cắt SC tại P. Suy ra giao tuyến của (α) và (SCD) là NP // SD.
+) Trong mặt phẳng (SBC), từ điểm P kẻ đường thẳng song song với BC // AD cắt SB tại Q. Suy ra giao tuyến của (α) và (SBC) là PQ // AD.
+) Trong mặt phẳng (SAB), nối M và Q. Suy ra giao tuyến của (α) và (SAB) là MQ // SA.
a) Xét từ giác MNPQ, có: MN // PQ nên MNPQ là hình thang.
Ta có: SA // MQ, MN // AD và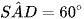 
nên 
.
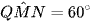Ta lại có: MN // AD, NP // SD và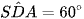 
nên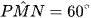 
.
Suy ra: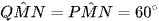 
.
Do đó tứ giác MNPQ là hình thang.
b)
+) Ta có ABCD là hình thoi và MN // AD //BC nên MN = a.
+) Trong tam giác ABC, có PQ // BC nên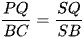 
(định lí Thales)
+) Trong tam giác SAB, có: MQ / SA nên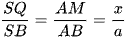 
(định lí Thales)
Do đó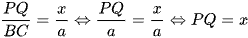 
+) Ta lại có: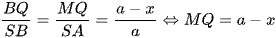 
+) Xét tam giác MHQ vuông tại H, có:
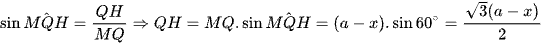
Vậy diện tích hình thang cân MNPQ là: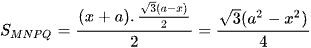 
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao