Giải bài tập Hoạt động khám phá 9 trang 41 Toán 12 Tập 2 | SGK Toán 12 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động khám phá 9 trang 41 Toán 12 Tập 2. Bài 1. Phương trình mặt phẳng. SGK Toán 12 - Chân trời sáng tạo
Đề bài:
Trong không gian Oxyz, cho mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 và điểm M0(x0; y0; z0). Gọi M1(x1; y1; z1) là hình chiếu vuông góc của M0 trên (α) (Hình 17).
a) Nêu nhận xét về phương của hai vectơ 
và 
= (A; B; C).
b) Tính 
theo A, B, C, D và tọa độ của M0.
c) Giải thích tại sao ta lại có đẳng thức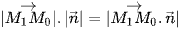 
.
d) Từ các kết quả trên suy ra cách tính 
.
Đáp án và cách giải chi tiết:
a) Vì M1(x1; y1; z1) là hình chiếu vuông góc của M0 trên (α) nên M1M0 ^ (α).
Do đó hai vectơ và = (A; B; C) cùng phương với nhau.
b) 
= Ax0 + By0 + Cz0 – Ax1 – By1 – Cz1.
Vì M1(x1; y1; z1) Î (α) nên ta có Ax1 + By1 + Cz1 + D = 0 ⇔ D = – Ax1 – By1 – Cz1.
Do đó 
= Ax0 + By0 + Cz0 + D.
c) Ta có 
.
Mà do hai vectơ 
và 
cùng phương với nhau nên 
hoặc 
.
+) Nếu 
thì 
.
+) Nếu 
thì 
.
Do đó 
d) Vì 
nên
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao