Giải bài tập Hoạt động khám phá 8 trang 53 Toán 12 Tập 2 | SGK Toán 12 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động khám phá 8 trang 53 Toán 12 Tập 2. Bài 2. Phương trình đường thẳng trong không gian. SGK Toán 12 - Chân trời sáng tạo
Đề bài:
Cho hai đường thẳng d và d' có vectơ chỉ phương lần lượt là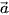 
= (2; 1; 3), 
= (3; 2; -8).
a) Nhắc lại định nghĩa góc giữa hai đường thẳng d và d' trong không gian.
b) Vectơ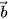 
= (-2; -1; -3) có phải là một vectơ chỉ phương của d không?
c) Giải thích tại sao ta lại có đẳng thức cos(d, d') = 
.
d) Nêu cách tìm côsin của góc giữa hai đường thẳng theo côsin của góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
Đáp án và cách giải chi tiết:
a) Góc giữa hai đường thẳng d và d' trong không gian, kí hiệu (d, d') là góc giữa hai đường thẳng a và b cùng đi qua một điểm và lần lượt song song hoặc trùng với d và d'.
b) 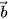= (-2; -1; -3) = 
. Do đó 
cũng là vectơ chỉ phương của đường thẳng d.
c) Vì 
lần lượt là vectơ chỉ phương của hai đường thẳng d và d' nên:
+) (d, d') = 
nếu 
.
+) (d, d') = 
nếu 
.
Do đó cos(d, d') = .
d) cos(d, d') = 
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao