Giải bài tập Bài 12 trang 60 Toán 12 Tập 2 | SGK Toán 12 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 12 trang 60 Toán 12 Tập 2. Bài 2. Phương trình đường thẳng trong không gian. SGK Toán 12 - Chân trời sáng tạo
Đề bài:
Bài 12 trang 60 Toán 12 Tập 2: Trong không gian Oxyz, cho hình lăng trụ đứng OBC.O'B'C' có đáy là tam giác OBC vuông tại O. Cho biết B(3; 0; 0), C(0; 1; 0), O'(0; 0; 2). Tính góc giữa:
a) Hai đường thẳng BO' và B'C;
b) Hai mặt phẳng (O'BC) và (OBC);
c) Đường thẳng B'C và mặt phẳng (O'BC)
Đáp án và cách giải chi tiết:
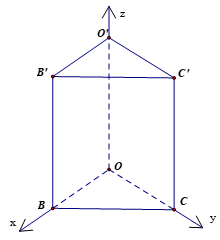
Chọn hệ trục như hình vẽ
O(0; 0; 0), B(3; 0; 0), C(0; 1; 0), O'(0; 0; 2), B'(3; 0; 2), C'(0; 1; 2).
a) Đường thẳng BO' nhận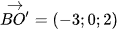 
làm vectơ chỉ phương.
Đường thẳng B'C nhận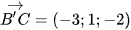 
làm vectơ chỉ phương.
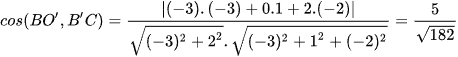
Suy ra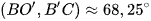 
.
b) Mặt phẳng (OBC) là (Oxy) nên nhận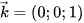 
làm vectơ pháp tuyến.
Mặt phẳng (O'BC) có phương trình đoạn chắn là: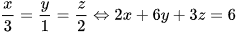 
có vectơ pháp tuyến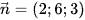 
.
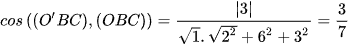Suy ra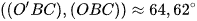 
c) Đường thẳng B'C nhận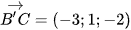 
làm vectơ chỉ phương.
Mặt phẳng (O'BC) có vectơ pháp tuyến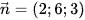 
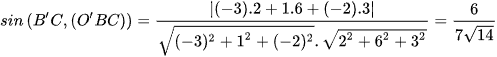
Suy ra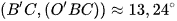 
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao