Giải bài tập HĐ2 trang 13 Toán 12 Tập 2 | SGK Toán 12 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập HĐ2 trang 13 Toán 12 Tập 2. Bài 12. Tích phân.. SGK Toán 12 - Kết nối tri thức
Đề bài:
Xét hình thang cong giới hạn bởi đồ thị 
, trục hoành và hai đường thẳng x = 1, x = 2. Ta muốn tính diện tích S của hình thang cong này.
a) Với mỗi x ∈ [1; 2], gọi S(x) là diện tích phần hình thang cong đã cho nằm giữa hai đường thẳng vuông góc với trục Ox tại điểm có hoành độ bằng 1 và x (H.4.5).
Cho h > 0 sao cho x + h < 2. So sánh hiệu S(x + h) – S(x) với diện tích hai hình chữ nhật MNPQ và MNEF (H.4.6). Từ đó suy ra 
.
b) Cho h < 0 sao cho x + h > 1. Tương tự phần a, đánh giá hiệu S(x) – S(x + h) và từ đó suy ra 
.
c) Từ kết quả phần a và phần b, suy ra với mọi h ≠ 0, ta có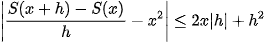 
.
Từ đó chứng minh 
, 
.
Người ta chứng minh được S'(1) = 1, S'(2) = 4, tức là S(x) là một nguyên hàm của 
trên [1; 2].
d) Từ kết quả của phần c, ta có 
. Sử dụng điều này với lưu ý S(1) = 0 và diện tích cần tính S = S(2), hãy tính S.
Gọi F(x) là một nguyên hàm tùy ý của f(x) = x2 trên [1; 2]. Hãy so sánh S và F(2) – F(1).
Đáp án và cách giải chi tiết:
a) Với h > 0, x + h < 2, kí hiệu 
và 
lần lượt là diện tích các hình chữ nhật MNPQ và MNEF, ta có: 
.
hay 
.
Suy ra
b) Với h < 0 và x + h > 1, kí hiệu và lần lượt là diện tích các hình chữ nhật MNPQ và MNEF, ta có
hay 
.
Suy ra .
c) Dựa vào kết quả của câu a, b ta suy ra với mọi 
, ta có:
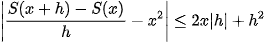
Suy ra 
, 
d) Vì S(1) = 0 nên 
Vậy 
Ta có 
Giả sử 
là một nguyên hàm của 
trên [1; 2].
Khi đó 
; 
. Ta thấy 
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao