Giải bài tập Bài 5 trang 106 Toán 11 Tập 1 | Toán 11 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 5 trang 106 Toán 11 Tập 1. Bài 2: Hai đường thẳng song song. Toán 11 - Chân trời sáng tạo
Đề bài:
Bài 5 trang 106 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành, AC và BD cắt nhau tại O. Gọi I là trung điểm của SO. Mặt phẳng ICD cắt SA, SB lần lượt tại M, N.
a) Hãy nói cách xác định hai điểm M và N. Cho AB = a. Tính MN theo a.
b) Trong mặt phẳng (CDMN), gọi K là giao điểm của CN và DM. Chứng minh SK // BC //AD.
Đáp án và cách giải chi tiết:
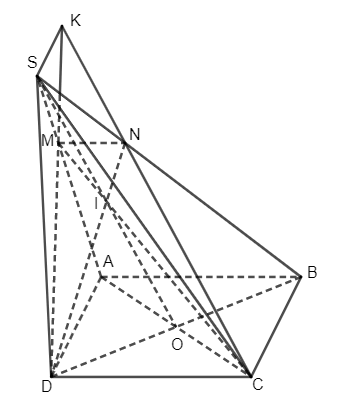
a) +) Trong mặt phẳng (SBD) có DI cắt SB tại N.
Mà DI ⊂ (ICD)
Do đó (ICD) cắt SB tại N.
+) Trong mặt phẳng (SAC) có CI cắt SA tại M.
Mà CI ⊂ (ICD)
Do đó (ICD) cắt SA tại M.
+)
b) Ta có:
(SAD) ∩ (ABCD) = AD
(SBC) ∩ (ABCD) = BC
(SAD) ∩ (SBC) = SK
Mà AD // BC
⇒ SK // AD // BC.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao