Mặt cầu trong không gian | SGK Toán 12 - Cánh diều
Mặt cầu trong không gian
Dưới đây là công thức Mặt cầu trong không gian
A. PHƯƠNG PHÁP GIẢI TOÁN
1) Lập phương trình mặt cầu:
• Để lập phương trình mặt cầu ta cần tìm tâm và bán kính R Khi đó phương trình mặt cầu có dạng: 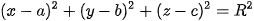
• Ngoài ra để lập phương trình mặt cầu ta có thể tìm các hệ số 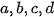 trong phương trình:
trong phương trình: 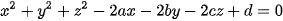 , với tâm , bán kính
, với tâm , bán kính 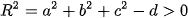
• Một mặt cầu được hoàn toàn xác định khi biết tâm và bán kính hoặc biết đường kính.
2) Vị trí tương đối giữa mặt cầu và mặt phẳng:
Cho mặt cầu tâm I, bán kính R và mặt phẳng 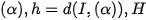 là hình chiếu của I lên mặt phẳng
là hình chiếu của I lên mặt phẳng
• 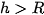 thì và mặt cầu không giao nhau.
thì và mặt cầu không giao nhau.
• 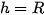 thì và mặt cầu tiếp xúc nhau tại H
thì và mặt cầu tiếp xúc nhau tại H
• 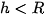 thì và mặt cầu cắt nhau theo giao tuyến là đường tròn tâm H, bán kính
thì và mặt cầu cắt nhau theo giao tuyến là đường tròn tâm H, bán kính 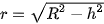
3) Vị trí tương đối giữa mặt cầu và đường thẳng:
Cho mặt cầu tâm , bán kính và đường thẳng 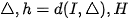 là hình chiếu của I lên mặt phẳng
là hình chiếu của I lên mặt phẳng
• 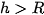 thì và mặt cầu không giao nhau.
thì và mặt cầu không giao nhau.
• 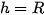 thì và mặt cầu tiếp xúc nhau tại Hay là tiếp tuyến của mặt cầu
thì và mặt cầu tiếp xúc nhau tại Hay là tiếp tuyến của mặt cầu
• 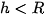 thì và mặt cầu cắt nhau tại hai điểm phân biệt A,B và H là trung điểm của dây cung , do đó:
thì và mặt cầu cắt nhau tại hai điểm phân biệt A,B và H là trung điểm của dây cung , do đó: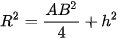
B. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH
Ví dụ 1. Trong không gian với hệ tọa độ , cho điểm và đường thẳng 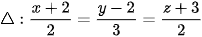 . Tính khoảng cách từ A đến Viết phương trình mặt cầu tâm A, cắt tại hai điểm B và C sao cho
. Tính khoảng cách từ A đến Viết phương trình mặt cầu tâm A, cắt tại hai điểm B và C sao cho
Đường thẳng qua 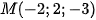 và có
và có  là VTCP.
là VTCP.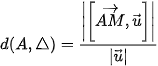
Gọi H là hình chiếu của A lên thì và là trung điểm của nên Vậy bán kính mặt cầu là 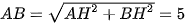
Nên phương trình mặt cầu là 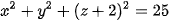
Ví dụ 2. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng có phương trình: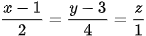 và mặt phẳng
và mặt phẳng 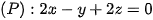 Viết phương trình mặt cầu có tâm thuộc đường thẳng , bán kính bằng và tiếp xúc với mặt phẳng
Viết phương trình mặt cầu có tâm thuộc đường thẳng , bán kính bằng và tiếp xúc với mặt phẳng
Gọi là mặt cầu cần tìm, là tâm.
Phương trình tham số đường thẳng 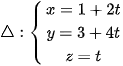 Vì
Vì 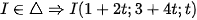
Ta có tiếp xúc với nên: 
• 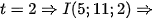 phương trình mặt cầu
phương trình mặt cầu 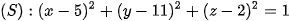
• 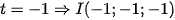 suy ra phương trình mặt cầu
suy ra phương trình mặt cầu 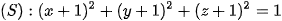
Ví dụ 3. Trong không gian với hệ tọa độ Đề các vuông góc cho và mặt phẳng
1. Lập phương trình mặt cầu tâm sao cho giao của với mặt phẳng là đường tròn có chu vi bằng
2. Chứng minh rằng mặt cầu nói trong phần 1 tiếp xúc với đường thẳng 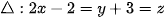
3. Lập phương trình mặt phẳng chứa đường thẳng và tiếp xúc với
Giải
1. Gọi , lần lượt là bán kính của mặt cầu và đường tròn
Ta có:  và
và 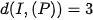 nên
nên 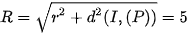
Vậy phương trình mặt cầu 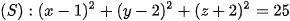
2. Đường thẳng có 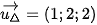 là VTCP và đi qua
là VTCP và đi qua 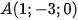 .
.
Suy ra 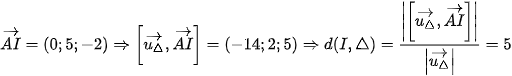
Vậy đường thẳng tiếp xúc với mặt cầu
Cách khác:
Phương trình tham số của 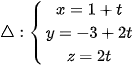 , thay vào phương trình mặt cầu , ta được:
, thay vào phương trình mặt cầu , ta được: 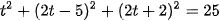
Suy ra mặt cầu và giao nhau tại một điểm 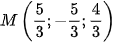
Vậy đường thẳng tiếp xúc với mặt cầu tại
3. Vì mặt phẳng chứa và tiếp xúc với mặt cầu nên là tiếp điểm của mặt phẳng và mặt cầu
Do đó là mặt phẳng đi qua và nhận 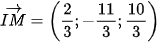 làm VTPT.
làm VTPT.
Vậy phương trình mặt phẳng 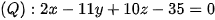
Ví dụ 4. Trong không gian với hệ tọa độ
1. Lập phương trình mặt cầu đi qua điểm và qua đường tròn là giao của mặt phẳng và mặt cầu 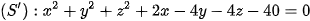
2. Viết phương trình mặt phẳng chứa 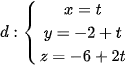 sao cho giao tuyến của mặt phẳng và mặt cầu là đường tròn có bán kính
sao cho giao tuyến của mặt phẳng và mặt cầu là đường tròn có bán kính
Giải
1.Vì mặt cầu đi qua đường tròn nên phương trình có dạng: 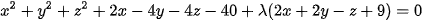
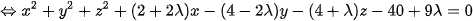
Vì 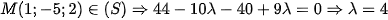
Vậy phương trình mặt cầu 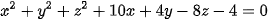
2. Đường thẳng d đi qua 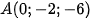 và có
và có 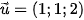 là VTCP.
là VTCP.
Phương trình của có dạng: 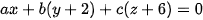
Hay 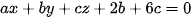
Trong đó 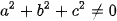 và
và 
Mặt cầu có tâm 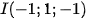 , bán kính
, bán kính
Theo giả thiết, ta suy ra 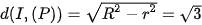
Do đó: 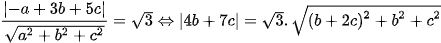

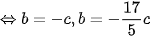
• ta chọn 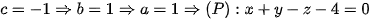
• 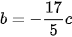 ta chọn
ta chọn 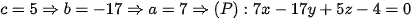
Ví dụ 5. Lập phương trình mặt phẳng biết:
1. chứa hai đường thẳng cắt nhau có phương trình: 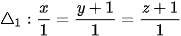 ,
, 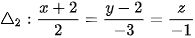
2. chứa hai đường thẳng song song có phương trình: 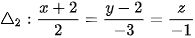 ,
, 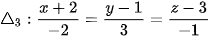
3. chứa đường thẳng 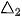 và cắt mặt cầu theo một đường tròn có bán kính bằng
và cắt mặt cầu theo một đường tròn có bán kính bằng 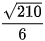
Giải
1. Đường thẳng 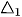 qua và
qua và 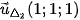
Đường thẳng 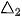 qua và
qua và 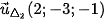
Cặp véc tơ chỉ phương của là 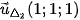 và
và 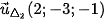 nên một véc tơ pháp tuyến của là
nên một véc tơ pháp tuyến của là 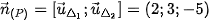
Phương trình mặt phẳng chứa hai đường thẳng 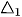 và
và 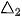 là
là 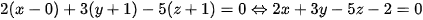
2. Đường thẳng 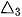 qua
qua 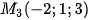 và
và 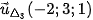
Cặp véc tơ chỉ phương của là 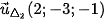 và
và 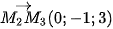 nên một véc tơ pháp tuyến của là
nên một véc tơ pháp tuyến của là 
Phương trình mặt phẳng chứa hai đường thẳng 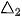 và
và 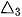 là
là 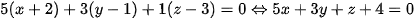
3. Vì chứa đường thẳng 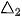 nên đi qua hai điểm thuộc
nên đi qua hai điểm thuộc 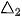 là điểm
là điểm 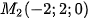 và
và 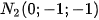
Phương trình mặt phẳng qua có dạng 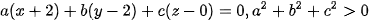
Vì qua 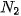 nên
nên
Mặt phẳng cắt mặt cầu theo giao tuyến là đường tròn có bán kính bằng 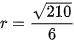 nên
nên 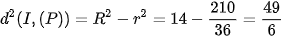
Do đó 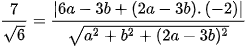
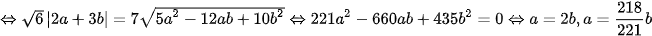
Nếu a=2b thì chọn  ta có
ta có 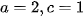 nên phương trình mặt phẳng
nên phương trình mặt phẳng 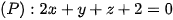
Nếu  thì chọn ta có
thì chọn ta có 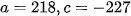 nên phương trình mặt phẳng
nên phương trình mặt phẳng 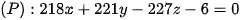
Vậy có hai mặt phẳng thỏa mãn là: 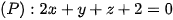 và
và 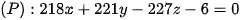
Các công thức liên quan:
Công thức tổng quát tính bán kính mặt cầu ngoại tiếp khối tứ diện và các trường hợp đặc biệt
Công thức tổng quát tính bán kính mặt cầu ngoại tiếp khối tứ diện và các trường hợp đặc biệt
Tổng hợp tất cả các công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện
Tổng hợp tất cả các công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện