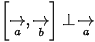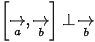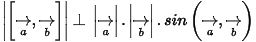Công thức tích có hướng của hai vecto và ứng dụng. | SGK Toán 12 - Chân trời sáng tạo
Công thức tích có hướng của hai vecto và ứng dụng.
Dưới đây là công thức Công thức tích có hướng của hai vecto và ứng dụng.
☞ Định nghĩa: Cho 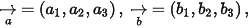 tích có hướng của
tích có hướng của 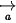 và
và 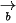 là
là
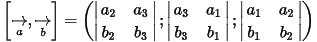
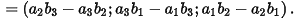
☞ Tính chất:
Lưu ý: Tích vô hướng của 2 vectơ là một số, tích có hướng của 2 vectơ là một vectơ.
- Điều kiện cùng phương của hai vectơ
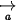 và
và 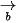 là
là 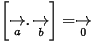 với
với 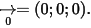
- Điều kiện đồng phẳng của ba vectơ
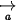 ,
, 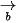 và
và 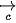 là
là 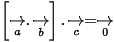
- Diện tích hình bình hành ABCD:
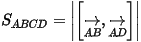
- Diện tích tam giác ABC:
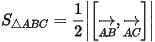
- Thể tích khối hộp:
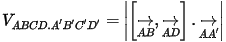
- Thể tích tứ diện:
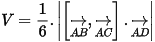
- Khoảng cách 2 đường thẳng AB; CD:
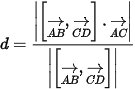
- Khoảng cách từ đỉnh đến đáy trong khối tứ diện:
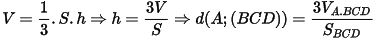
VÍ DỤ
Câu 1: Trong không gian Oxyz, tam giác ABC với A(2;1;1), B(5;3;6), C(-1;2;3) có diện tích là?
Hướng dẫn giải
Ta có: I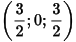 là trung điểm của BD, suy ra D(1;-1;1).
là trung điểm của BD, suy ra D(1;-1;1).
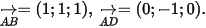
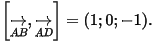
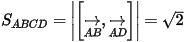 (đvdt).
(đvdt).
Câu 2: Trong không gian Oxyz, cho 4 điểm A(2;0;2), B(1;-1;-2), C(-1;1;0), D(-2;1;2).Thể tích của khối tứ diện ABCD bằng?
Hướng dẫn giải
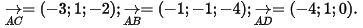
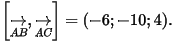
Thể tích khối tứ diện là: 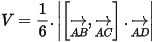
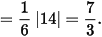
Câu 3: (Bình Giang-Hải Dương 2019) Trong không gian với hệ tọa độ Oxyz , cho bốn điểm A(0;0;2), B(3;0;5), C(1;1;0), A(4;1;2). Độ dài đường cao của tứ diện ABCD hạ từ đỉnh D xuống mặt phẳng ABC là?
Hướng dẫn giải
Gọi DH là độ dài đường cao của tứ diện ABCD hạ từ đỉnh D xuống mặt phẳng ABC.
Công thức tính thể tích tứ diện ABCD là: 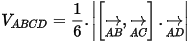
Công thức tính diện tích tam giác 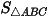 là:
là: 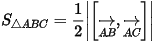
Mặt khác 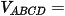
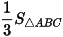 .DH nên
.DH nên
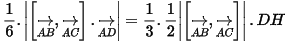
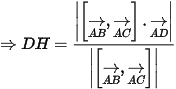
Ta có:
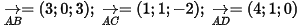
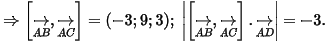
Nên 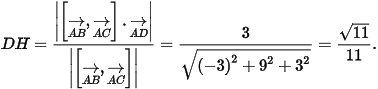
Các công thức liên quan:
Công thức tọa độ của vecto trong không gian (lớp 12)
Công thức tọa độ của vecto trong không gian (lớp 12)
Ứng dụng phương pháp tọa độ giải bài toán hình học không gian
Ứng dụng phương pháp tọa độ giải bài toán hình học không gian
[Lớp 10] Biểu thức toạ độ của phép cộng hai vectơ, phép trừ hai vectơ, phép nhân một số với một vectơ
Biểu thức toạ độ của phép cộng hai vectơ, phép trừ hai vectơ, phép nhân một số với một vectơ
[Lớp 12] Cách tìm toạ độ của một vectơ vuông góc với hai vectơ cho trước
Cách tìm toạ độ của một vectơ vuông góc với hai vectơ cho trước