Cách chứng minh 3 điểm thẳng hàng, 3 đường thẳng đồng quy | Toán 11 - Chân trời sáng tạo

A. Phương pháp giải

- Để chứng minh 3 điểm A; B; C thẳng hàng ta chứng minh 3 điểm đó cùng thuộc 1 đường thẳng hoặc chứng minh 3 điểm đó là điểm chung của hai mặt phẳng (α) và (β) - Khi đó chúng cùng thuộc giao tuyến của 2 mặt phẳng (α) và (β).

- Để chứng minh ba đường thẳng đồng quy ta có thể làm theo những cách sau:

   + Cách 1: chứng minh giao điểm của hai đường này là điểm chung của hai mặt phẳng mà giao tuyến là đường thẳng thứ ba

   + Cách 2: Dựa vào định lí: Ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến khi đó; ba giao tuyến đó đồng quy hoặc đôi một song song

B. Ví dụ minh họa

Ví dụ 1: Cho tứ diện ABCD. Gọi M; N lần lượt là trung điểm của AB và CD. Mặt phẳng (P) qua MN và cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?

A. I; A; C        B. I; B; D         C. I; A; B        D. I; C; D

Lời giải

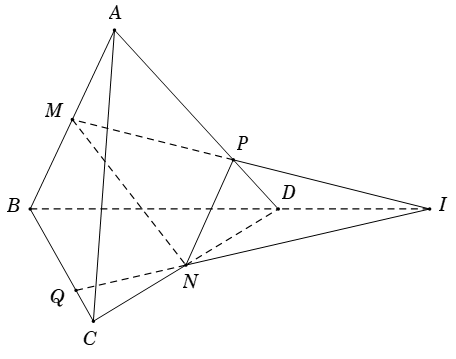
Ta có: 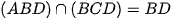 (1)

Lại có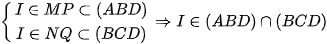

Từ (1) và (2) suy ra: I ∈ BD hay 3 điểm I; B; D thẳng hàng

Chọn B.

Ví dụ 2: Cho tứ diện SABC. Gọi L; M; N lần lượt là các điểm trên các cạnh SA; SB và AC sao cho LM không song song với AB và LN không song song với SC. Mặt phẳng (LMN) cắt các cạnh AB; BC và SC lần lượt tại K; I; J. Ba điểm nào sau đây thẳng hàng?

A. K; I và J        B. M; I và J        C. N ; I và J        D. M; K và J

Lời giải

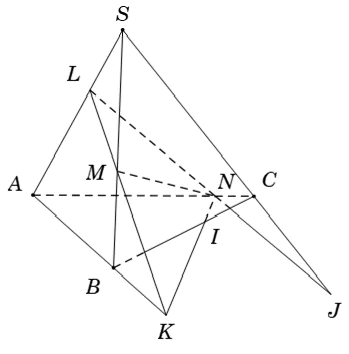
Ta có

- M ∈ SB suy ra M isin; (LMN) ∩ (SBC)    (1)

- I ∈ BC ⊂ (SBC) và I ∈ NK ⊂ (LMN)

⇒ I ∈ (LMN) ∩ (SBC)   (2)

- J ∈ SC ⊂ (SBC) và J ∈ LN ⊂ (LMN)

⇒ J ∈ (LMN) ∩ (SBC)     (3)

Vậy M ; I; J thẳng hàng vì cùng thuộc giao tuyến của mp (LMN) và (SBC)

Chọn B

Ví dụ 3: Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD; M là trung điểm CD; I thuộc đoạn AG; BI cắt mp (ACD) tại J. Chọn mệnh đề sai

A. Giao tuyến của (ACD) và (ABG) là AM

B. 3 điểm A; J; M thẳng hàng.

C. J là trung điểm của AM.

D. Giao tuyến của mp(ACD) và (BDJ) là DJ.

Lời giải

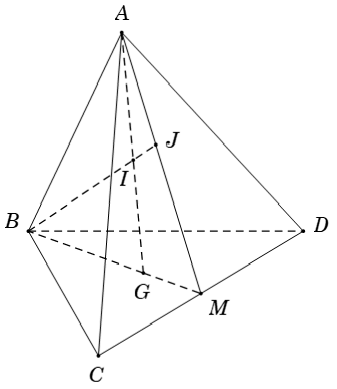
Ta xét các phương án:

   + Ta có: A là điểm chung thứ nhất giữa hai mp (ACD) và mp (GAB)    (1)

Do M là giao điểm của BG và CD nên: 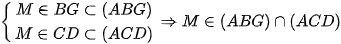(2)

Từ (1) và (2) suy ra: giao tuyến của (ABG) và (ACD) là AM ⇒ A đúng.

+ Ta có 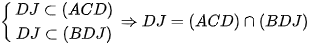⇒ D đúng

+ Điểm I di động trên AG nên J có thể không phải là trung điểm của AM.⇒ C sai

Chọn C.

Ví dụ 4: Cho tứ diện ABCD. Gọi E; F; G là các điểm lần lượt thuộc các cạnh AB; AC; BD sao cho EF cắt BC tại I; EG cắt AD tại H. Ba đường thẳng nào sau đây đồng quy?

A. CD; EF; EG          B. CD; IG; HF          C. AB; IG; HF          D, AC; IG; BD

Lời giải

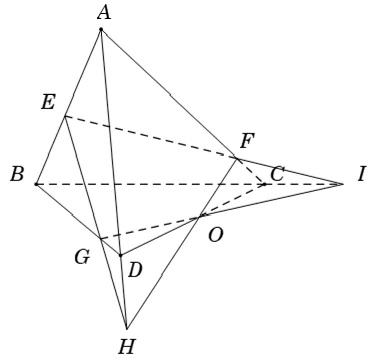
Gọi O là giao điểm của HF và IG . Ta có

- O ∈ HF mà HF ⊂ (ACD) suy ra O ∈ (ACD)

- O ∈ IG mà IG ⊂ (BCD) suy ra O ∈ (BCD)

Do đó O ∈ (ACD) ∩ (BCD)    (1)

Mà (ACD) ∩ (BCD) = CD   (2)

Từ (1) và (2), suy ra O ∈ CD.

Vậy ba đường thẳng CD; IG; HF đồng quy tại O.

Chọn B

Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD không phải là hình thang. Trên cạnh SC lấy điểm M . Gọi N là giao điểm của SD và mp (AMB). Mệnh đề nào sau đây đúng?

A. Ba đường thẳng AB; CD; MN đôi một song song

B. Ba đường thẳng AB; CD; MN đôi một cắt nhau

C. Ba đường thẳng AB; CD; MN đồng quy

D. Ba đường thẳng AB; CD; MN cùng thuộc một mặt phẳng

Lời giải

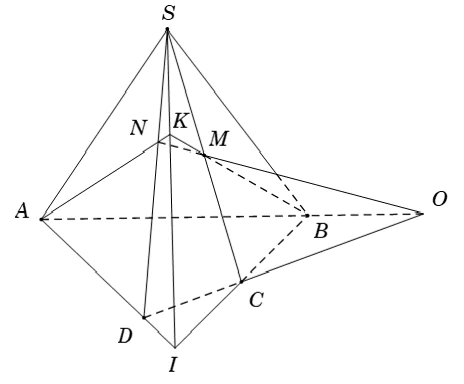
- Trong mp (ABCD) gọi I là giao điểm của AD và BC

Trong mp (SBC), gọi K là giao điểm của BM và SI

Trong mp (SAD); gọi N là giao điểm của AK và SD

Khi đó N là giao điểm của đường thẳng SD với mp(AMB)

- Gọi O là giao điểm của AB và CD. Ta có:

   + O ∈ AB mà AB ⊂ (AMB) suy ra O ∈ (AMB)

   + O ∈ CD mà CD ⊂ (SCD) suy ra O ∈ (SCD)

⇒ O ∈ (AMB) ∩ (SCD)    (1)

Mà MN = (AMB) ∩ (SCD)    (2)

Từ (1) và (2) , suy ra O ∈ MN.

Vậy ba đường thẳng AB; CD và MN đồng quy.

Chọn C

Ví dụ 6: Cho tứ diện ABCD có G là trọng tâm tam giác BCD, M là trung điểm CD, I là điểm trên đoạn thẳng AG, BI cắt mặt phẳng (ACD) tại J. Khẳng định nào sau đây sai?

A. AM = (ACD) ∩ (ABG)

B. A; J; M thẳng hàng

C. J là trung điểm AM

D. DJ = (ACD) ∩ (BDJ)

Lời giải

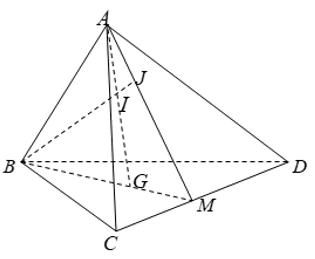
Chọn C

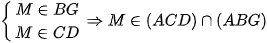nên 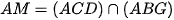. Vậy A đúng.

+ Ba điểm A; J và M cùng thuộc hai mặt phẳng phân biệt (ACD) và (ABG) nên A; J; M thẳng hàng, vậy B đúng

+ Vì I là điểm tùy ý trên AG nên J không phải lúc nào cũng là trung điểm của AM.