Giải bài tập Bài 7 trang 60 Toán 9 Tập 1: | Toán 9 - Cánh diều

Hướng dẫn giải chi tiết từng bước bài tập Bài 7 trang 60 Toán 9 Tập 1: . Bài 2. Một số phép tính về căn bậc hai của số thực.. Toán 9 - Cánh diều

Đề bài:

Cho tam giác đều ABC có độ dài cạnh là a. Tính độ dài đường cao AH của tam giác ABC theo a.

Đáp án và cách giải chi tiết:

Xét ∆ABC đều có AH là đường cao nên đồng thời là đường trung tuyến của tam giác, do đó H là trung điểm của BC.

Suy ra HC = $\frac{B C}{2} = \frac{a}{2} .$

Xét ∆AHC vuông tại H, theo định lí Pythagore, ta có:

AC² = AH² + HC²

Suy ra AH² = AC² - HC² = a² - ${(\frac{a}{2})}^{2} = a^{2} - \frac{a^{2}}{4} = \frac{3 a^{2}}{4} .$

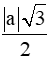
Do đó AH = $\sqrt{\frac{3 a^{2}}{4}} = \frac{\sqrt{3 a^{2}}}{\sqrt{4}}$ = Bài 7 trang 60 Toán 9 Tập 1 Cánh diều | Giải Toán 9 = $\frac{a \sqrt{3}}{2}$ (vì a > 0).

Vậy độ dài đường cao AH của tam giác ABC là $\frac{a \sqrt{3}}{2}$ .

Nguồn: giaitoanhay.com

Tổng số đánh giá:

Xếp hạng: / 5 sao

Bài tập liên quan:

Khởi động trang 55 Toán 9 Tập 1:

Hoạt động 1 trang 55 Toán 9 Tập 1:

Luyện tập 1 trang 55 Toán 9 Tập 1:

Hoạt động 2 trang 56 Toán 9 Tập 1:

Luyện tập 2 trang 56 Toán 9 Tập 1:

Luyện tập 3 trang 57 Toán 9 Tập 1:

Hoạt động 4 trang 57 Toán 9 Tập 1:

Luyện tập 4 trang 58 Toán 9 Tập 1:

Luyện tập 5 trang 59 Toán 9 Tập 1:

Hoạt động 5 trang 58 Toán 9 Tập 1:

Hoạt động 3 trang 57 Toán 9 Tập 1:

Bài 1 trang 59 Toán 9 Tập 1:

Bài 2 trang 59 Toán 9 Tập 1:

Bài 3 trang 59 Toán 9 Tập 1:

Bài 4 trang 59 Toán 9 Tập 1:

Bài 5 trang 59 Toán 9 Tập 1:

Bài 6 trang 60 Toán 9 Tập 1:

Bài 8 trang 60 Toán 9 Tập 1:

Bài 9 trang 60 Toán 9 Tập 1:

Giải bài tập Toán 9 - Cánh diều

Xem tất cả Bài 1. Phương trình quy về phương trình bậc nhất một ẩn. Bài 2. Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn. Bài 3. Giải hệ hai phương trình bậc nhất hai ẩn. Bài tập cuối chương 1

Xem tất cả Bài 1. Bất đẳng thức. Bài 2. Bất phương trình bậc nhất một ẩn. Bài tập cuối chương II. HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM. Chủ đề 1. Làm quen với bảo hiểm.

Xem tất cả Bài 1. Căn bậc hai và căn bậc ba của số thực Bài 2. Một số phép tính về căn bậc hai của số thực. Bài 3. Căn thức bậc hai và căn thức bậc ba của biểu thức đại số. Bài 4. Một số phép biến đổi căn thức bậc hai của biểu thức đại số. Bài tập cuối chương 3

Xem tất cả Bài 1. Tỉ số lượng giác của góc nhọn. Bài 2. Một số hệ thức về cạnh và góc trong tam giác vuông. Bài 3. Ứng dụng của tỉ số lượng giác của góc nhọn. Bài tập cuối chương 4

Xem tất cả Bài 1. Đường tròn. Vị trí tương đối của hai đường tròn Bài 2. Vị trí tương đối của đường thẳng và đường tròn Bài 3. Tiếp tuyến của đường tròn Bài 4. Góc ở tâm. Góc nội tiếp Bài 5. Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên Bài tập cuối chương 5

Xem tất cả Bài 1. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ Bài 2. Tần số. Tần số tương đối Bài 3. Tần số ghép nhóm. Tần số tương đối ghép nhóm Bài 4. Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố Bài tập cuối chương 6 HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM. Chủ đề 2. Mật độ dân số.

Xem tất cả Bài 1. Hàm số y = ax² (a ≠ 0) Bài 2. Phương trình bậc hai một ẩn. Bài 3. Định lí Viète. Bài tập cuối chương 7

Xem tất cả Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác Bài 2. Tứ giác nội tiếp đường tròn Bài tập cuối chương 8

Xem tất cả Bài 1. Đa giác đều. Hình đa giác đều trong thực tiễn Bài 2. Phép quay Bài tập cuối chương 9

Xem tất cả Bài 1. Hình trụ Bài 2. Hình nón Bài 3. Hình cầu Bài tập cuối chương 10 HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM. Chủ đề 3. Tạo đồ dùng dạng hình nón, hình trụ.