Giải bài tập Bài 101 trang 42 SBT Toán 12 Tập 1 | SBT Toán 12 - Cánh diều (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 101 trang 42 SBT Toán 12 Tập 1. Bài tập cuối chương 1. SBT Toán 12 - Cánh diều (SBT)
Đề bài:
Cho hàm số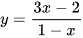 
.
a) Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1. 
b) Đồ thị hàm số có tiệm cận ngang là đường thẳng y = 3.
c) Điểm M nằm trên đồ thị hàm số có hoành độ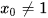 
thì tung độ 
.
d) Tích khoảng cách từ điểm M bất kì nằm trên đồ thị hàm số đến hai đường tiệm cận của đồ thị hàm số đó bằng 1.
Đáp án và cách giải chi tiết:
|
a) Đ |
b) S |
c) Đ |
d) Đ |
Ta có: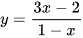
Tập xác định: 
.
Có 
, 
.
Do đó, đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1.
, 
.
Do đó, đồ thị hàm số có tiệm cận ngang là đường thẳng y = −3.
Có 
thay vào hàm y ta được:
.
Lấy 
thuộc đồ thị hàm số, ta có:
Khoảng cách từ M đến đường tiệm cận đứng x = 1 là: 
.
Khoảng cách từ M đến đường tiệm cận ngang y = −3 là: 
.
Ta có 
.
Vậy tích khoảng cách từ điểm M bất kì nằm trên đồ thị hàm số đến hai đường tiệm cận của đồ thị hàm số đó bằng 1.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao