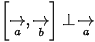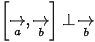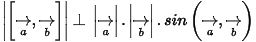Công thức tích có hướng của hai vecto và ứng dụng. | SGK Toán 12 - Cánh diều
Công thức tích có hướng của hai vecto và ứng dụng.
Dưới đây là công thức Công thức tích có hướng của hai vecto và ứng dụng.
☞ Định nghĩa: Cho 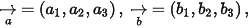 tích có hướng của
tích có hướng của 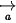 và
và 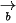 là
là
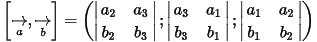
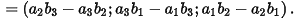
☞ Tính chất:
Lưu ý: Tích vô hướng của 2 vectơ là một số, tích có hướng của 2 vectơ là một vectơ.
- Điều kiện cùng phương của hai vectơ
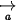 và
và 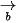 là
là 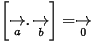 với
với 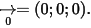
- Điều kiện đồng phẳng của ba vectơ
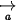 ,
, 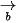 và
và 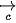 là
là 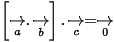
- Diện tích hình bình hành ABCD:
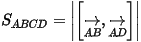
- Diện tích tam giác ABC:
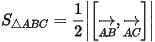
- Thể tích khối hộp:
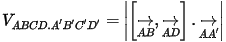
- Thể tích tứ diện:
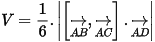
- Khoảng cách 2 đường thẳng AB; CD:
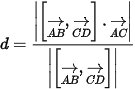
- Khoảng cách từ đỉnh đến đáy trong khối tứ diện:
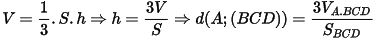
VÍ DỤ
Câu 1: Trong không gian Oxyz, tam giác ABC với A(2;1;1), B(5;3;6), C(-1;2;3) có diện tích là?
Hướng dẫn giải
Ta có: I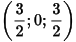 là trung điểm của BD, suy ra D(1;-1;1).
là trung điểm của BD, suy ra D(1;-1;1).
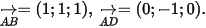
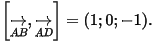
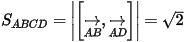 (đvdt).
(đvdt).
Câu 2: Trong không gian Oxyz, cho 4 điểm A(2;0;2), B(1;-1;-2), C(-1;1;0), D(-2;1;2).Thể tích của khối tứ diện ABCD bằng?
Hướng dẫn giải
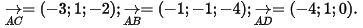
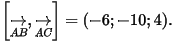
Thể tích khối tứ diện là: 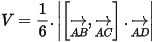
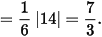
Câu 3: (Bình Giang-Hải Dương 2019) Trong không gian với hệ tọa độ Oxyz , cho bốn điểm A(0;0;2), B(3;0;5), C(1;1;0), A(4;1;2). Độ dài đường cao của tứ diện ABCD hạ từ đỉnh D xuống mặt phẳng ABC là?
Hướng dẫn giải
Gọi DH là độ dài đường cao của tứ diện ABCD hạ từ đỉnh D xuống mặt phẳng ABC.
Công thức tính thể tích tứ diện ABCD là: 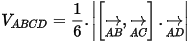
Công thức tính diện tích tam giác 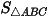 là:
là: 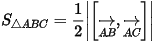
Mặt khác 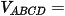
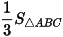 .DH nên
.DH nên
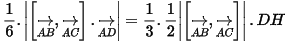
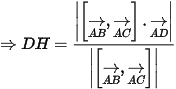
Ta có:
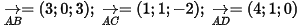
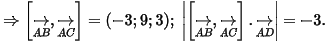
Nên 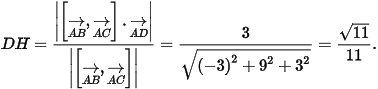
Các công thức liên quan:
Công thức tọa độ của vecto trong không gian (lớp 12)
Công thức tọa độ của vecto trong không gian (lớp 12)